R.Schuster: Grundkurs Biomathematik.
Teubner-Studientext

Wiederholungen und Einführung in Mathematica

• Erste Auswertung von Beobachtungsdaten mit Mathematica, grafische Darstellungen
• Quadratische Funktionen und MathematicaKomplexe Zahlen
• Elementare Funktionen
• Potenzfunktionen
• Exponential- und Logarithmusfunktionen
• Winkelfunktionen
• Hyperbolische Winkelfunktionen
• Polynome
• Wiederholung zur Differential- und Integralrechnung
• Kurvendiskussion mit Mathematica
• Reihenentwicklungen mit Mathematica, Taylorreihen

Wachstumsmodelle. Gewöhnliche Differentialgleichungen mit einer unabhängigen Variablen

• Exponentielles Wachstum
• Wachstum mit Sättigungsverhalten. Logistisches Wachstum. Verhulstkurve. Gleichgewichte und Stabilität in mathematischen Modellen
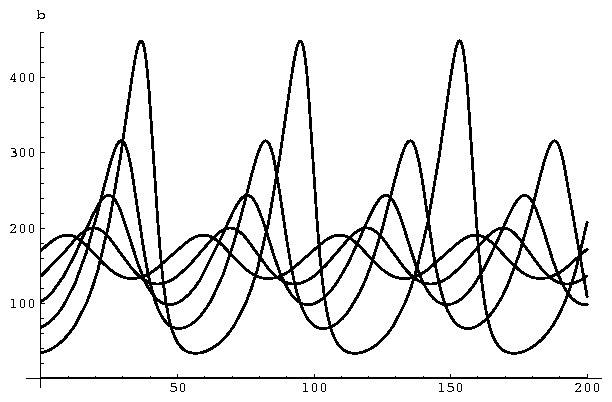
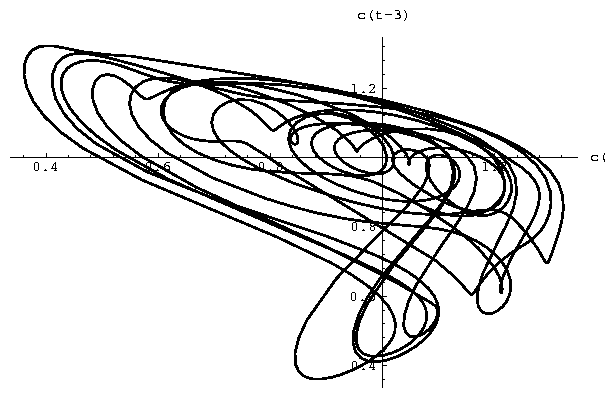
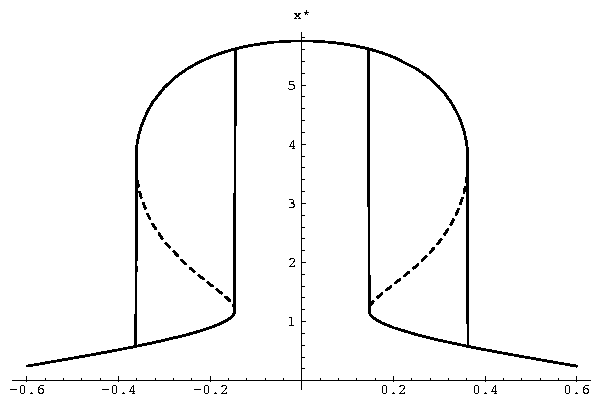
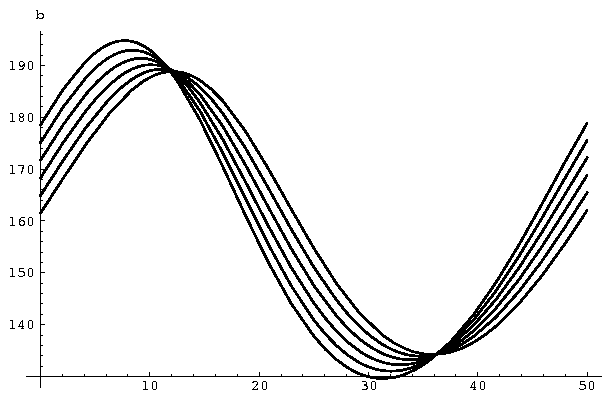
• Verzögerungsmodelle. Dynamische Krankheiten in der Physiologie

Lineare Gleichungssysteme

• Einführung
• Matrizen
• Determinanten
• Inverse Matrizen
• Lösungsstruktur linearer Gleichungssysteme
• Eigenwerte und Eigenvektoren
• Anwendungen in der Populationsgenetik

Populationen mit Wechselwirkungen, Systeme gewöhnlicher Differentialgleichungen

• Das Räuber-Beute-Modell von Lotka-Volterra
• Ein Räuber-Beute-Modell mit Grenzzyklus
• Konkurrenzverhalten zweier Arten mit gleicher Nahrungsquelle. Volterrasches Exklusionsprinzip
• Oszillierende chemische und biochemische Systeme. Die Belousov-Zhabotinskii-Reaktion
• Erregbarkeit von Nervenmembranen im Differentialgleichungsmodell. Das FitzHugh-Namugo-Modell in der Hodgkin-Huxley-Theorie

Dynamik von Infektionskrankheiten

• Die SEIR-Klasseneinteilung
• Untersuchung des SIR-Modells
• Anwendung des SIR-Modells auf Influenza und Pest

Kompliziertere Anwendungen mit Computerlösungen

• Michaelis-Menten-Theorie in der Enzymkinetik
• Unterschiedliche Zeitskalen
• Rückkopplungsmechanismen im Zusammenwirken von mRNA, Enzymen und Proteinen
• Schwarze Löcher in der Biologie

Räumlich-zeitliche Wirkungsausbreitung. Partielle Differentialgleichungen

• Diffusions- und Wärmeleitungsgleichung
• Reaktions-Diffusions-Gleichungen. Wellenförmige Wirkungsausbreitung
• Fourierreihen. Ein Rand-Anfangswert-Problem

Statistik

• Statistische Maßzahlen. Berechnungen und grafische Darstellungen mit Mathematica
• Diskrete und stetige Zufallsgrüßen, Realisierung von Zufallsgrößen als "verallgemeinertes Würfeln", Unabhängigkeit
• Erwartungswert, Varianz und Verteilungsfunktion
• Normalverteilung
• Binomialverteilung
• Poissonverteilung
• Chi-Quadrat, F- und Student-t-Verteilung
• Konfidenzintervalle
• Der t-Test nach Student, weitere Tests zu normalverteilten Ausgangsdaten
• Der Chi-Quadrat-Anpassungstest
• Der Vierfelder-Chi-Quadrat-Test
• Der Kolmogoroff-Smirnoff-Test
• Varianzanalyse
• Lineare Regression, Kovarianzkoeffizient
• Nichtlineare Regression

Fraktale

• Von den "Monsterkurven der Analysis" zu den Fraktalen
• Juliamengen und Mandelbrotmenge
• Komplexe Cantorsche Mengen