Mathematica als Taschenrechner
Man kann im Dialog elementare Rechnungen wie im Taschenrechner ausführen lassen.
Ein Beispiel: durch [SHIFT]-[RETURN] erhält man das Ergebnis.
![]()
![]()
Mathematica kann automatisch beliebig große Zahlen (mit den üblichen Einschränkungen durch Speicherpatz und Rechengeschwindigkeit) berechnen .
![]()
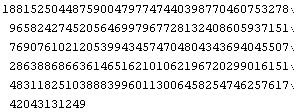
Unter Verwendung der "palettes" kann die mathematische Standardbezeichnung verwendet werden.
![]()
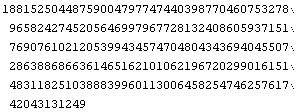
Mathematica kann die Eigenwerte einer Matrix berechnen.
![]()
![]()
Es können Eigenwerte und Eigenfunktionen berechnet werden.
![]()
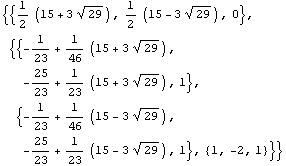
Eine wichtige Eigenschaft von Mathematica ist es, mit Zahlen und mit Formeln rechnen zu können ("Formelmanipulation").
Mit Mathematica kann man parameterabhängig eine Gleichung lösen.
![]()
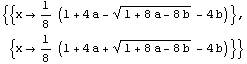
Es kann können mit Mathematica unbestimmte Integrale gelöst werden (innerhalb der behandelbaren Funktionsklasse), wobei eine gewisse Vorsicht in der Überprüfung der der Ergebnisse angemessen ist.
![]()
![(x^(1/2) (a + 1/x + x)^(1/2) (2 (a + 2 x) (1 + a x + x^2)^(1/2) - (-4 + a^2) Log[a + 2 (x + (1 + a x + x^2)^(1/2))]))/(8 (1 + a x + x^2)^(1/2))](HTMLFiles/index_14.gif)
Mit Mathematica können 2D und 3D Grafiken erzeugt werden.
Ein 2D-Plot einer Funktion:
![]()
![[Graphics:HTMLFiles/index_16.gif]](HTMLFiles/index_16.gif)
![]()
Ein 3D-Plot einer Funktion in x und y, die Option "PlotPoints→30" spezifiziert die Auflösung. .
![]()
![[Graphics:HTMLFiles/index_19.gif]](HTMLFiles/index_19.gif)
![]()
Über die Taschenrechner-Funktionalität hinaus lassen sich umfangreichere Berechnungen in kurzer Notation durchführen.
Erzeugung einer 200×200 - Matrix aus Zufallszahlen. Mit dem Semikolon am Ende wird die Ausgabe (aus Platzgründen) unterdrückt.
![]()
Berechnung und grafische Darstellung aller Eigenwerte der Zufallsmatrix (Auf aktuellen PC Rechnezeit im Sekundenbereich).
![]()
![[Graphics:HTMLFiles/index_23.gif]](HTMLFiles/index_23.gif)
![]()
Mathematica kann große Zahlen behandeln, hier die Fakultät von 500.
![]()

Mathematica kann numerische Berechnungen mit vorgegebener Präzision durchführen, z.B. die Berechnung von pi auf 1000 Stellen.
![]()

Mathematica kann Polynome faktorisieren:
![]()
![]()
Mathematica kann Ausdrücke vereinfachen, wobei es unterschiedliche Sichtweisen geben kann, was "einfach" ist. Gegebenenfalls muß die gewünschte Form näher spezifiziert werden. Das Zeichen % steht für den vorangegangenen Ausdruck.
![]()
![]()
Mathematica enthält eine umfangreiche Sammlung an Algotithmen.
Mathematica kann Nullstellen und Integrale numerisch berechnen.
![]()
![]()
![]()
![]()
![]()
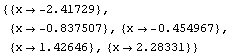
Mathematica enthält state-of-the-art-Algorithmen zur Faktorisierung von natürlichen Zahlen. Als Ergebnis erhält man eine Liste von Faktoren und Exponenten.
![]()
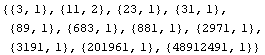
Erzeungung einer 2D - Tabelle:
![]()

Anzeige in Matrix-Form:
![]()

Berechnung des Nullraumes einer Matrix:
![]()
![]()
Mathematica kann Differentialgleichungen numerisch und symbolisch (innerhalb bestimmter Funktionsklassen) lösen.
Hier löst Mathematica eine nichtlineare Differentialgleichung numerisch. Das Ergebnis liegt in Form einer Interpolationsfunktion ("interpolating function") vor.
![NDSolve[{x ' '[t] + 2 x[t]^3 == Sin[t], x[0] == x '[0] == 0}, <br /> ... bsp; x, {t, 0, 50}]](HTMLFiles/index_47.gif)
![]()
Das Ergebnis kann dann grafisch dargestellt werden. Durch /. wird die berechnete Lösung eingesetzt.
![]()
![[Graphics:HTMLFiles/index_50.gif]](HTMLFiles/index_50.gif)
![]()
Mathematica kann Eigenwerte auch parameterabhängig berechnen.
![]()
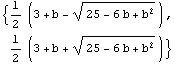
Die Mathematica-Ausgaben könen als Eingaben für weitere Berechnungen verwendet werden.
2D-Darstellung der parameterabhängigen Eigenwerte.
![]()
![[Graphics:HTMLFiles/index_55.gif]](HTMLFiles/index_55.gif)
![]()
Nullstellenberechnung dazu:
![]()
![]()
Parameterabhängige Potenzreihendarstellung von Funktionen:
![]()
![Sin[b]/x + Cos[b] - 1/2 Sin[b] x - 1/6 Cos[b] x^2 + 1/24 Sin[b] x^3 + 1/120 Cos[b] x^4 - 1/7 ... in[b] x^7)/40320 + (Cos[b] x^8)/362880 - (Sin[b] x^9)/3628800 - (Cos[b] x^10)/39916800 + O[x]^11](HTMLFiles/index_60.gif)
Prinzahlen und Kurvenanpassungen.
Liste der ersten 100 Prinzahlen.
![]()

Kurvenanpassung zu den Primzahlen:
![]()
![]()
Addition der angpaßten Funktionswerte:
![]()
![]()
Zum Vergleich die Originalwerte:
![]()
![]()
Darstellung der Differenzen zwischen Summen der Originalwerte und Summe der angepaßten Werte bis 100:
![ListPlot[Table[Sum[Evaluate[Fit[Table[Prime[i], {i, imax}], {Log[x], x, x^2}, x], {x, imax}]] - Underoverscript[∑, i = 1, arg3] Prime[i], {imax, 2, 100}], PlotJoinedTrue]](HTMLFiles/index_69.gif)
![[Graphics:HTMLFiles/index_70.gif]](HTMLFiles/index_70.gif)
![]()
Umwandlung von Ausdrücken.
Komplexere Ausdrücke können in verschiedenen Frmen dargestellt werden. Mathematica bietet eine Reihe von Funktionalitäten zur Konvertierung.
Ein gegebener Ausdruck, der umgeformt werden soll:
e = (x - 1)^3 (2 + x) / ((1 + x) (x - 3)^3)
![]()
Zerlegung in eine Summe, wobei Zähler und Nenner gekürzt werden, der verbleibende Ausdruck im Nenner nicht ausmultipziert ist:
Expand[e]
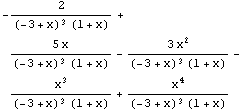
ExpandAll multipliziert zusätzlich den Nenner aus.
ExpandAll[e]
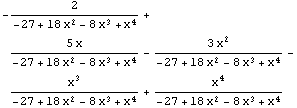
Mit Together erhalten wir einen Ausdruck mit Hauptnenner.
Together[%]
![]()
Apart ergibt die Partialbruchzerlegung:
Apart[%]
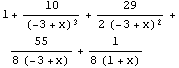
Factor ergibt durch Faktorierung den Anfangsausdruck.
Factor[%]
![]()
Zusammenfassungen können bezüglich verschiedener Variabler von Interesse sein:
Ein algebraischer Ausdruck in zwei Variablen:
v = Expand[(3 + 2 x)^3 (x + 2 y)^2]
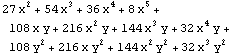
Collect[v, x]
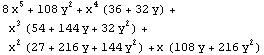
Collect[v, y]
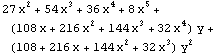
Faktorisieren der nicht von y abhängigen Terme:
FactorTerms[v, y]
![]()
Eine Reihe weiterer Umformungen beziehen sich auf trigonometrische Funktionen.
Entwicklung von Vielfachen des Arguments, wie z.B. (2 x) in Ausdrücke des Arguments x:
TrigExpand[Cot[x] Sin[2x]]
![]()
Faktorisierung trigonometrischer Ausdrücke:
TrigFactor[%]
![]()
Reduzierung durch Vielfache des Arguments:
TrigReduce[%]
![]()
Zerlegung in Real- und Imaginärteil unter der Voraussetzung, daß x und y reell sind:
ComplexExpand[ Cos[x + I y] ]
![]()
Zerlegung mit komplexen Werten von x und y:
ComplexExpand[ Sin[x + I y], {x, y} ]
![]()
Ermittlung von Teilausdrücken.
e = Expand[(1 + 3x + 4y^2)^3]
![]()
Koeffizient von x in e.
Coefficient[e, x]
![]()
Exponent[expr, y] gibt die höchste Potenz von y an, die in expr auftritt.
Exponent[e, y]
![]()
Der vierte Term in e.
Part[e, 4]
![]()
Zerlegung eines Bruches.
r = (1 + x)^2/(2 (2 - y)^3)
![]()
Nenner:
Denominator[r]
![]()
Numerator[r]
![]()
| Created by Mathematica (October 23, 2005) |